

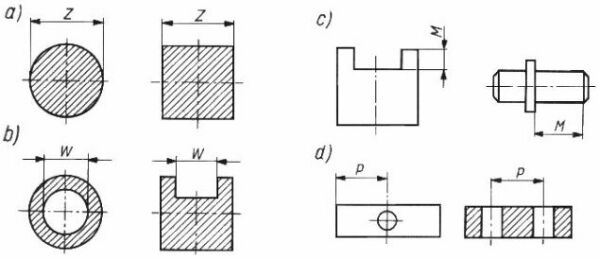

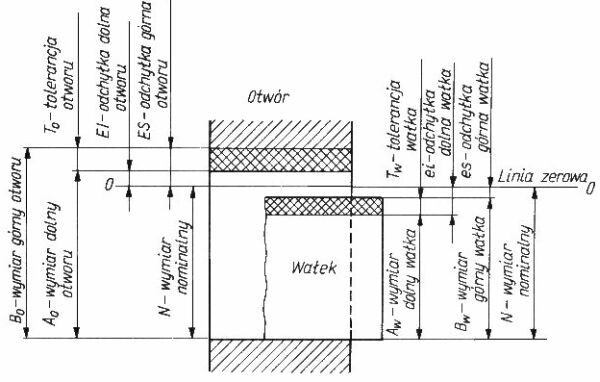
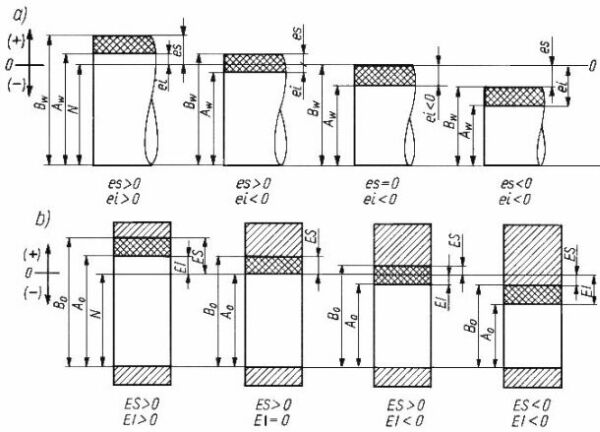
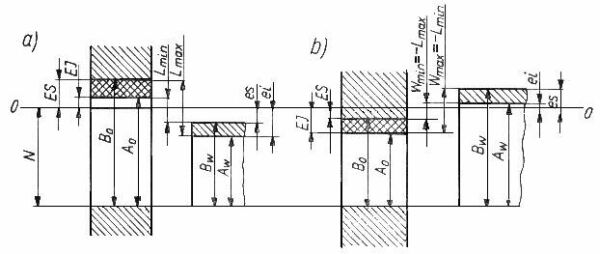

W trosce o komfort korzystania z naszego serwisu chcemy dostarczac Ci coraz lepsze uslugi. By moc to robic prosimy, abys wyrazil zgode na dopasowanie tresci marketingowych do Twoich zachowan w serwisie. Zgoda ta pozwoli nam czesciowo finansowac rozwoj swiadczonych uslug.
Pamietaj, ze dbamy o Twoja prywatnosc. Nie zwiekszamy zakresu naszych uprawnien bez Twojej zgody. Zadbamy rowniez o bezpieczenstwo Twoich danych. Wyrazona zgode mozesz cofnac w kazdej chwili.